Analyse Multi Variable des prix du FM
- Emmanuel Gilson,
- Nicolas Cugier,
- Christian Duréault,
- Teodora Petrişor,
- Hélia Pouyllau, Université Paris-Saclay & Thales
Juin 2017
Dans le cadre du contrat Copernic 1, 18 prestations de Facility Management sont définies et contractualisées par le biais des Service-Level Agreements (SLA). Ces prestations concernent 45 sites français de Thales d’une taille supérieure à 2000m². Chaque prestation est chiffrée séparément par Vinci Facilities, le prestataire. Le cadre contractuel standardisé et la récolte des données effectuée par la Direction des Services Généraux de Thales permettent de disposer d’une base de données suffisamment complète pour envisager des méthodes d’analyse statistique. Différentes variables de cette base de données ont été identifiées comme a priori pertinentes : la surface tertiaire, industrielle, data-center, salles blanches, le nombre d’occupants, le niveau d’accord entre les managers Vinci Facilities et Thales d’un site, la vétusté du site, le nombre d’équipements par SLA et par site, et la localisation d’un site à Paris ou Province. Après avoir défini et présenté les indicateurs utilisés pour analyser les résultats, nous tentons de prédire les prix des SLA en utilisant une méthode de régression linéaire classique. Puis plusieurs études d’impact sont conduites pour savoir si les variables d’accord, de vétusté et localisation à Paris ou Province ont un impact sur le prix des SLA.
1. Données de départ
Le contrat Copernic gère les prestations de services généraux de 45 sites, nous disposons de la plupart des variables citées pour ces sites. Toutefois, on observe beaucoup de « 0 » que ce soit pour la variable dépendante ou indépendante (surface de salles blanches, de data-center…). Ainsi, le SLA Gestion technique du Bâtiment ne concerne que 22 des sites les plus récents soit moins de la moitié de l’ensemble. L’information contenue dans ces variables reste donc limitée. De façon générale, un ensemble de 45 observations demeure faible pour mettre en évidence une causalité. Même si la régression linéaire est une méthode relativement stable, on s’attend à une variance élevée dans les estimations.
Données considérées :
| SLA | VARIABLES | SITES |
|---|---|---|
| Appareils élévateurs | Entente | AUBAGNE |
| CFO Electricité Courant Fort | Nombre d’équipements | BLAGNAC |
| Contrôles réglementaires | Nombre d’occupants | BREST |
| Courrier et Colis | Surface data Center | BRETIGNY |
| CVC Chauffage Ventilation Clim | Surface salles Blanches | BRIVE |
| Déchets | Surface tertiaire | CANNES |
| Entretien du Bâtiment | Surface totale | CAZAUX |
| Espaces Verts | Vétusté | CHATELLERAULT la Brelandière |
| GTB Gestion technique du Bâtiment | CHATELLERAULT M. Dassault | |
| Installations de sûreté | CHATOU | |
| Management | CHOLET | |
| Manutention | ELANCOURT BUREAUPLUS | |
| Nettoyage | ELANCOURT EUCLIDE 2 | |
| Portes et Barrières | ELANCOURT NUNGESSER | |
| Sécurité Incendie | ETR ETRELLES | |
| FLEURY LES AUBRAIS | ||
| GENNEVILLIERS | ||
| JOUY EN JOSAS | ||
| LA DEFENSE CARPE DIEM | ||
| LA FERTE SAINT AUBIN | ||
| LAMBERSART | ||
| LAVAL SAPHIR | ||
| LE HAILLAN | ||
| LIMOURS | ||
| MASSY | ||
| MERU | ||
| MOIRANS POMMARIN 460 | ||
| MOIRANS POMMARIN 760 | ||
| OSNY | ||
| PALAISEAU | ||
| PESSAC | ||
| RUNGIS | ||
| SAINT HEAND | ||
| THONON | ||
| TOULOUSE CHAMPOLLION | ||
| TOULOUSE EISENHOWER | ||
| VALDOLINES | ||
| VALENCE | ||
| VELIZY 2 HELIOS | ||
| VELIZY 2 MARCEL DASSAULT | ||
| VELIZY LE BOIS | ||
| VENDOME INDUSTRIE | ||
| VENDOME MONS | ||
| VILLEBON | ||
| YMARE |
Des incertitudes dans les mesures de certaines variables existent. C’est notamment le cas pour les surfaces. Les mesures de surfaces sont faites par les managers de site, qui ont pour certains des définitions des surfaces data-center et salles blanches potentiellement assez différentes. La variable nombre de bâtiments est également à utiliser avec précaution, étant construite par le service juridique de la direction immobilière Thalès et servant donc un but juridique (décomposition par propriétaires, fonctions…).
On rappelle la décomposition de la surface totale : Tertiaire, Industriel, Logistique, Plateforme et Vide. La surface Industrielle contient la surface de salles blanches, et la surface de plateforme contient la surface data center. Les surfaces salles blanches et data center sont plus pertinentes que plateforme et industriel car on peut être certain qu’elles impliquent plus de coûts en termes de prestations de services généraux, alors que la pertinence de surface industrielle et plateforme peut varier selon la définition qu’en a le manager de site.
L’accord entre les managers Vinci Facilities et Thales d’un site comprend 4 niveaux : les niveaux 1 à 3 qualifient le niveau d’accord de manière croissante, le niveau 4 correspond aux nouvelles relations (moins de 6 mois de l’arrivée au poste d’un nouveau manager de site). La vétusté varie également de 1 à 3, et est une fonction de l’année de mise en service du site, le niveau 3 correspondant aux sites les plus anciens. Les variables de vétusté et d’accord ont été transformées en variables binaires.
Le nombre d’équipements par site pour les SLA Courants Forts (CFO), Chauffage Ventilation Climatisation (CVC) et Entretien du Bâtiment ont également été réunis à partir des listes d’équipements construites par les managers de site. Les chiffres ont pu être réunis pour 31 sites pour les 3 SLA cités. Des listes d’équipements ne sont pas disponibles sur certains sites ; d’autres ont des informations manquantes. Compte tenu du manque important de données sur ces variables, on sera amené à les traiter à part.
La localisation des sites à Paris ou Province est une variable binaire : 1 pour les sites d’Ile-de-France et 0 pour les autres.
Nous avons eu accès à un certain nombre d’informations supplémentaires que nous avons choisi de ne pas utiliser :
- Le nombre de bâtiments : en plus d’être très corrélé à la surface totale du site, cette variable provient du service juridique de la Direction Immobilière et le dénombrement juridique des bâtiments n’est pas pertinent pour notre cas.
- Le nombre d’Equivalent Temps Plein facturé par Vinci Facilities : Cette variable est également très corrélée à la surface. De plus, elle constitue un terme du contrat et est donc issue d’une négociation. Or, notre but est de fournir des éléments pour la négociation, et non pas d’analyser les résultats de la négociation. Ainsi, le nombre d’ETP a plus sa place dans le groupe des variables à prédire (avec les prix) que les prédicteurs.
2. Indicateurs utilisés :
Pour la corrélation :
L’indice de corrélation de Pearson : 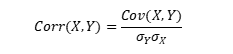
Avec et les écarts-types des vecteurs Y et X et Cov (X,Y) la covariance entre les 2 vecteurs. Cet indice, compris entre -1 et 1, permet d’observer la part des variations partagées par 2 séries par rapport à leur variabilité totale. Il peut aussi indiquer, s’il est très élevé, si des variables apportent la même information. A partir de 0.8, on peut considérer que les 2 variables apportent la même information, et qu’introduire les 2 variables dans un même modèle peut conduire à de la colinéarité.
Pour la régression :
Le coefficient de détermination : ![]()
Le R² correspond à la part de la variance de la variable dépendante expliquée par les variables indépendantes. Il peut être utilisé comme mesure de la qualité de la régression.
Le coefficient de régression ^β : il mesure la relation entre une variable indépendante et la variable dépendante. On distingue β qui est la valeur du coefficient estimé, et ^β qui est le ‘vrai’ coefficient (non mesurable).
La p-value est un indicateur associé à un test d’hypothèse. Une hypothèse standard qui est testée est celle de la nullité du coefficient de régression (β=0). Si la p-value est inférieure à 5 % (seuil standard), cela signifie que les observations ne correspondent pas à l’hypothèse et donc que la nullité du coefficient est statistiquement peu probable selon cet échantillon. C’est un indicateur de la significativité statistique de l’existence d’une relation entre une variable indépendante et la variable dépendante. La p-value ne rend pas compte du signe ni de l’ampleur d’une relation entre 2 variables.
L’intervalle de confiance : ![]()
Avec le ^β coefficient de régression, σ l’erreur moyenne de la régression, n le nombre d’observations et 1.96 la valeur de la statistique de Student pour un risque d’erreur de 5 %.
L’intervalle de confiance du coefficient de régression représente les valeurs pour lesquelles la différence entre le paramètre de la population (le ‘vrai’ coefficient) et le paramètre estimé n’est pas significative à 5 % de risque d’erreur. Si la p-value d’un coefficient est inférieure à 5 %, alors l’intervalle de confiance associé n’inclut pas 0. Cependant, il peut quand même être très large. Ainsi, si l’on veut faire de la prédiction avec un modèle, des p-values inférieures à 5 % ne sont pas suffisantes, il faut des intervalles de confiance relativement restreints. Cet indicateur sera donc un de nos principaux moteurs de décision dans le choix d’un modèle.
3. Corrélations entre variables
Nous allons mettre en évidence les coefficients de corrélations linéaires de Pearson entre les variables continues (surfaces, occupants et nombre de bâtiments). Ces valeurs vont nous permettre d’identifier les variables très corrélées entre elles, et ainsi d’écarter les doublons, c’est-à-dire les variables apportant la même information. L’utilité de cette méthode est uniquement méthodologique : elle permet de décorréler les variables indépendantes tout en évitant de procéder à une analyse en composantes principales, qui repose sur des hypothèses strictes et rend difficile l’interprétation des résultats finaux en transformant les variables d’entrée.
On note que la variable surface de data center contient trop de 0 pour calculer des indices de corrélation.
Indices de corrélation pour les surfaces, le nombre d’occupants et le nombre de bâtiments
| Variable | Bureaux | Occupants | Salles Blanches | Surface Totale |
|---|---|---|---|---|
| Bureaux | 1.0** | 0.78** | 0.17 | 0.64** |
| Occupants | 0.78** | 1.0** | 0.47** | 0.81** |
| Salles Blanches | 0.17 | 0.47** | 1.0** | 0.5** |
| Nb Bâtiments | 0.21 | 0.29* | 0.17 | 0.72** |
| Surface Totale | 0.64** | 0.81** | 0.5** | 1.0** |
Les astérisques (*) correspondent à la valeur de la p-value : Un * derrière l’indice de corrélation signifie que la p-value associée est inférieure à 0.10 et donc qu’il est significativement différent de 0 avec un risque d’erreur de moins de 10%, ** signifie que la p-value est inférieure à 0.05 et donc que l’indice est significatif à un seuil de 5%. Une absence de * signifie que l’indice n’est pas significatif.
Lecture : L’indice de corrélation entre nombre d’occupants et surface de bureaux est de 0.78 et est significatif à 5 % de risque d’erreur.
Les indices significatifs sont positifs et assez élevés. A noter que les différentes surfaces sont positivement corrélées. Ainsi, on n’observe pas de « spécialisations » des sites : les sites ne sont pas uniquement industriels, ou uniquement constitués de salles blanches, data-center … ce qui serait représenté par un indice de corrélation négatif, mais ont plutôt des parties destinés à la production et une autre à l’administration.
Quelques indices de corrélation très élevés sont à noter, notamment entre surface totale et nombre d’occupants, et occupants et bureaux. Des corrélations si élevées peuvent provoquer de la colinéarité et rendre un modèle instable. Ainsi, introduire ces variables dans une même spécification peut rendre des résultats incertains. Les indices significatifs sont positifs et assez élevés. A noter que les différentes surfaces sont positivement corrélées. Ainsi, on n’observe pas de « spécialisations » des sites : les sites ne sont pas uniquement industriels, ou uniquement constitués de salles blanches, data-center … ce qui serait représenté par un indice de corrélation négatif, mais ont plutôt des parties destinés à la production et une autre à l’administration.
Indices de corrélation pour les nombres d’équipements et la surface totale
| Variable | Equipements CVC | Equipements CFO | Equipements Entretien Bâtiment | Equipements Sécu Incendie |
|---|---|---|---|---|
| Equipements CVC | 1.0** | 0.62** | 0.66** | 0.64** |
| Equipements CFO | 0.62** | 1.0** | 0.75** | 0.42** |
| Equipements Entretien Bâtiment | 0.66** | 0.75** | 1.0** | 0.53** |
| Equipements Sécu Incendie | 0.64** | 0.42** | 0.53** | 1.0** |
Les corrélations sont là aussi fortes, significatives et positives, que ce soit entre les équipements par SLA ou entre les nombres d’équipements et la surface totale
4. Présentation des calculs de régression
Dans cette partie, l’objectif est d’établir un modèle utilisant des variables pertinentes pour chaque SLA afin de produire des prédictions aussi précises que possibles. Pour cela, nous utiliserons l’outil de régression linéaire, pour lequel l’équation est de type :
![]()
Où y est le vecteur des observations de la variable dépendante (le prix du SLA), X est la matrice des vecteurs des observations des variables indépendantes, ^β est le vecteur des coefficients de régression estimés et est le vecteur des erreurs du modèle, c’est-à-dire la différence entre la valeur réelle Yi et la valeur prédite 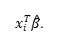
La méthode OLS (Original Least Squares) consiste à déterminer un coefficient de régression linéaire pour chaque variable en minimisant le carré de la différence entre la valeur réelle de la variable dépendante et la valeur estimée grâce au coefficient. Pour cela, l’estimateur non biaisé et convergent (sous les bonnes conditions) du coefficient est :
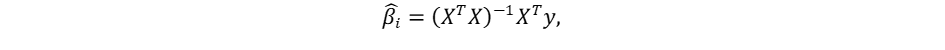 Où Xτ est la transposée de la matrice Χ.
Où Xτ est la transposée de la matrice Χ.
Dans un premier temps, nous cherchons à évaluer l’impact sur les prix des différentes variables identifiées jusqu’ici : les surfaces, l’accord, la vétusté, la localisation du site à région parisienne ou Province, le nombre de bâtiments par site et le nombre d’occupants. Nous allons procéder à autant de régressions qu’il y a de SLA. Nous allons tenter de constater l’existence ou non d’un effet sur le prix, l’ampleur et le signe de l’effet, sa significativité statistique… Pour cela, nous utiliserons les métriques suivantes : coefficients de régression, p-values, intervalles de confiance, indices de corrélation et R2.
Compte tenu de la faible taille de l’échantillon (45 sites), nous avons dû restreindre assez fortement le nombre de variables à introduire dans notre modèle. Ainsi, un maximum de 2 variables a été retenu, ceci pour éviter les problèmes de conditionnement de la matrice (XτX)-¹ . Nous présentons ci-dessous les modèles les plus efficaces : les p-values doivent être inférieures à 1%, et les intervalles de confiance les plus restreints, mais les variables doivent également maximiser le R2.
Les 2 premiers critères p-values et intervalles de confiance sont primordiaux pour pouvoir utiliser nos résultats dans un but prédictif, c’est-à-dire réutiliser nos modèles pour des sites nouveaux ou ne faisant pas partie de notre échantillon. Le R2 est un indicateur utile et simple à interpréter pour mesurer la qualité générale de l’estimation, mais il est moins pertinent pour la prédiction. En-dessous de 0.8, l’estimation est considérée comme incomplète : il manque une ou plusieurs variables pour expliquer le prix dont nous ne disposons pas.
5. Résultats obtenus :
Diagnostic des régressions et prédictions
Appareils Elévateurs Total | |||||
Variables | Coefficient | p_values | Borne Inf Conf | Borne Sup Conf | R Squared |
Nombre d’Occupants | 25.941 | 0.000 | 22.042 | 29.840 | 0.803 |
| |||||
CFO Total | |||||
Variables | Coefficient | p_values | Borne Inf Conf | Borne Sup Conf | R Squared |
Surface Totale | 4.021 | 0.000 | 3.010 | 5.032 | 0.910 |
Surface Bureaux | 2.944 | 0.002 | 1.155 | 4.732 | |
| |||||
Contrôles Réglementaires | |||||
Variables | Coefficient | p_values | Borne Inf Conf | Borne Sup Conf | R Squared |
Surface Totale | 1.387 | 0.000 | 1.046 | 1.728 | 0.901 |
Surface Bureaux | 0.752 | 0.016 | 0.148 | 1.355 | |
| |||||
Courrier et Colis Total | |||||
Variables | Coefficient | p_values | Borne Inf Conf | Borne Sup Conf | R Squared |
Nombre d’Occupants | 38.485 | 0.000 | 29.635 | 47.334 | 0.787 |
Surface de Datacenter | 29.318 | 0.000 | 14.837 | 43.799 | |
| |||||
CVC Total | |||||
Variables | Coefficient | p_values | Borne Inf Conf | Borne Sup Conf | R Squared |
Surface Totale | 8.053 | 0.000 | 7.349 | 8.758 | 0.923 |
| |||||
Déchets Total | |||||
Variables | Coefficient | p_values | Borne Inf Conf | Borne Sup Conf | R Squared |
Nombre d’Occupants | 16.848 | 0.000 | 9.305 | 24.391 | 0.621 |
Surface salles blanches | 5.655 | 0.002 | 2.245 | 9.066 | |
| |||||
Entretien du Bâtiment | |||||
Variables | Coefficient | p_values | Borne Inf Conf | Borne Sup Conf | R Squared |
Surface Totale | 3.003 | 0.000 | 2.137 | 3.869 | 0.905 |
Surface Bureaux | 3.097 | 0.000 | 1.564 | 4.629 | |
| |||||
Espaces Verts Total | |||||
Variables | Coefficient | p_values | Borne Inf Conf | Borne Sup Conf | R Squared |
Surface Totale | 1.549 | 0.000 | 1.318 | 1.781 | 0.816 |
Surface Salles Blanches | -8.093 | 0.000 | -11.025 | -5.161 | |
| |||||
GTB Total | |||||
Variables | Coefficient | p_values | Borne Inf Conf | Borne Sup Conf | R Squared |
Surface Bureaux | 0.477 | 0.000 | 0.295 | 0.659 | 0.865 |
Surface Salles Blanches | 8.276 | 0.000 | 6.972 | 9.580 | |
| |||||
Installations Sûreté Total | |||||
Variables | Coefficient | p_values | Borne Inf Conf | Borne Sup Conf | R Squared |
Surface Totale | 0.572 | 0.000 | 0.351 | 0.794 | 0.382 |
| |||||
Management de Site Total | |||||
Variables | Coefficient | p_values | Borne Inf Conf | Borne Sup Conf | R Squared |
Nombre d’Occupants | 100.573 | 0.000 | 65.731 | 135.414 | 0.909 |
Surface Bureaux | 4.451 | 0.000 | 2.253 | 6.649 | |
| |||||
Manutention Total | |||||
Variables | Coefficient | p_values | Borne Inf Conf | Borne Sup Conf | R Squared |
Nombre d’Occupants | 64.819 | 0.000 | 54.501 | 75.138 | 0.785 |
| |||||
Nettoyage Total | |||||
Variables | Coefficient | p_values | Borne Inf Conf | Borne Sup Conf | R Squared |
Nombre d’Occupants | 315.298 | 0.000 | 290.176 | 340.421 | 0.956 |
Surface de data-center | 70.129 | 0.001 | 29.019 | 111.238 | |
| |||||
Portes et Barrières Total | |||||
Variables | Coefficient | p_values | Borne Inf Conf | Borne Sup Conf | R Squared |
Nombre d’Occupants | 14.267 | 0.000 | 10.387 | 18.146 | 0.802 |
Surface Salles Blanches | 4.238 | 0.000 | 2.484 | 5.993 | |
| |||||
Sécurité Incendie Total | |||||
Variables | Coefficient | p_values | Borne Inf Conf | Borne Sup Conf | R Squared |
Nombre d’Occupants | 60.755 | 0.000 | 53.091 | 68.419 | 0.912 |
Surface de data-center | 30.989 | 0.000 | 18.448 | 43.531 | |
| |||||
6. Etudes d’impact complémentaires
Les variables étudiées ici sont l’accord, la vétusté, les nombres d’équipements par SLA et la localisation des sites à Paris ou Province. Ces variables ont fait l’objet d’une étude préalable et ont été jugées inutiles dans le cas de la prédiction. Elles peuvent néanmoins avoir un impact sur le prix, mais pas suffisamment significatif pour être des prédicteurs pertinents. Nous allons nous attacher à déterminer si ces variables ont un impact sur les prix de SLA. Pour cela, nous allons régresser les prix des SLA par les variables d’intérêt (accord, vétusté…) puis nous allons observer la valeur de la p-value. On rappelle que la p-value teste l’hypothèse selon laquelle le coefficient de régression de la variable d’intérêt est nul. Une p-value inférieure à 0.05 signifie que l’on rejette cette hypothèse et donc que la variable a un impact significatif sur les prix.
L’accord :
Nous avons à notre disposition une variable caractérisant l’accord entre les managers Thales et Vinci Facilities pour chaque site. On s’attend à ce qu’un meilleur accord entre les deux managers implique, par une communication plus soutenue, une réduction du prix des prestations c’est-à-dire de trouver un coefficient de régression positif et significatif pour l’accord.
La variable accord est une variable qualitative non ordonnée : ses valeurs correspondent à des classes (de 1 à 4) et pas à des valeurs numériques (comme la surface). Dans la régression, ces variables doivent être transformées en 4 variables binaires (que l’on appelle aussi « dummies ») pour être traitées comme variables indépendantes. Seules 3 des 4 variables binaires seront introduites dans le modèle de régression car la 4e variable est nécessairement une combinaison linéaire des 3 autres vecteurs.
Nous utiliserons la variable de surface totale comme variable de contrôle : comme nous avons vu l’importance non négligeable de la surface dans la détermination des prix des SLA, nous introduisons la surface totale pour éviter que les coefficients des variables d’accord ne capturent les variations des prix dues aux variations de surface. Pour chaque régression, cela nous donne donc 4 variables : les 3 variables binaires caractérisant l’accord et la variable de contrôle. Cela constitue un nombre de dimensions élevé pour un échantillon aussi restreint, mais nous sommes contraints par la nature de la variable d’accord.
A l’issue des calculs, on constate que les résultats ne montrent pas de relation solide entre accord et prix. Les variables d’accord affichent une forte colinéarité. Une variable colinéaire est une variable qui peut être obtenue par une combinaison linéaire d’une ou plusieurs autres variables. Ainsi, la variable colinéaire apporte une information déjà comprise dans les autres variables. En plus d’être inutile, la variable colinéaire rend la matrice des observations mal conditionnée et difficilement inversable. En cas de colinéarité parfaite, le processus de régression ne peut pas être mené à bout. Dans le cas où il existe de la colinéarité imparfaite, cela rend le modèle très instable. Le nombre de conditionnements reflète cette instabilité, puisqu’il montre à quel point les résultats peuvent changer avec un changement mineur des paramètres. Il est ici supérieur à 70 000. On considère généralement qu’un nombre de conditionnement supérieur à 10 montre une colinéarité forte des variables, et donc une instabilité des résultats de même ampleur. Cela se traduit par des coefficients estimés dispersés, et donc des p-values très élevées.
Les p-values, ces valeurs qui caractérisent la significativité statistique sont toutes très élevées. On rappelle qu’une p-value est comprise entre 0 et 1, où 0 signifie que l’on peut rejeter l’hypothèse de non-significativité et 1 que l’on peut l’accepter. Voici le tableau des p-values pour tous les prix et pour chaque variable indépendante (surface, accord…) :
| Sites | Surface Totale | Accord 1 | Accord 2 | Accord 3 |
|---|---|---|---|---|
| Management de Site Total | 0.000 | 0.728 | 0.046 | 0.160 |
| GTB Total | 0.000 | 0.059 | 0.236 | 0.600 |
| CVC Total | 0.000 | 0.908 | 0.424 | 0.876 |
| CFO Total | 0.000 | 0.489 | 0.107 | 0.925 |
| Sécurité Incendie Total | 0.000 | 0.722 | 0.151 | 0.877 |
| Installations de Sûreté Total | 0.056 | 0.004 | 0.066 | 0.097 |
| Contrôles Réglementaires Total | 0.000 | 0.003 | 0.053 | 0.072 |
| Entretien du Bâtiment Total | 0.000 | 0.574 | 0.480 | 0.239 |
| Appareils Elévateurs | 0.000 | 0.065 | 0.214 | 0.968 |
| Portes et Barrières Total | 0.000 | 0.971 | 0.504 | 0.253 |
| Espaces Verts Total | 0.000 | 0.018 | 0.105 | 0.368 |
| Courrier et Colis total | 0.000 | 0.103 | 0.980 | 0.286 |
| Nettoyage Total | 0.000 | 0.006 | 0.581 | 0.168 |
| Déchets Total | 0.000 | 0.379 | 0.231 | 0.170 |
| Manutention Total | 0.000 | 0.050 | 0.361 | 0.562 |
La surface totale du site est, comme attendu, très significative. En revanche les variables d’accord ont des p-values très élevées, ce qui signifie que, de façon générale, on ne peut pas conclure de façon positive sur l’existence d’un effet de l’accord sur les prix des SLA. Il est nécessaire de mettre ces résultats en perspective : cette méthode ne permet pas de conclure que l’accord n’a pas d’effet sur le prix. De plus, il faut analyser l’effet de l’accord sur le prix hors-forfait, qui est plus susceptible d’être affecté par l’accord entre managers.
La vétusté :
Nous nous intéressons à l’impact de la vétusté d’un site sur les prix des SLA. On peut s’attendre à ce qu’un site ancien coûte plus cher, surtout pour les SLA Multi Techniques (CVC, CFO, Installations de Sûreté…) mais également pour les SLA Multi Services : un site ancien peut demander plus de travail de nettoyage, par sa vétusté ou sa conception obsolète (très décentralisée par exemple).
La variable de vétusté est une variable catégorielle allant de 1 à 3, du plus récent au plus ancien. Comme pour l’accord, nous allons devoir discrétiser cette variable. Comme nous l’avons vu avec la variable d’accord, les vecteurs à valeurs binaires semblent provoquer de la colinéarité dans nos modèles.
Voici le tableau des p_values des variables d’accord :
| SLA | Surface Totale | Vétusté 1 | Signe vétusté 3 | Vétusté 3 |
|---|---|---|---|---|
| Management de Site Total | 0.00 | 0.18 | + | 0.02 |
| GTB Total | 0.00 | 0.78 | – | 0.91 |
| CVC Total | 0.00 | 0.84 | + | 0.01 |
| CFO Total | 0.00 | 0.62 | + | 0.01 |
| Sécurité Incendie Total | 0.00 | 0.59 | + | 0.07 |
| Installations de Sûreté Total | 0.00 | 0.50 | + | 0.35 |
| Contrôles Réglementaires Total | 0.00 | 0.64 | + | 0.02 |
| Entretien du Bâtiment Total | 0.00 | 0.78 | + | 0.05 |
| Appareils Elévateurs | 0.00 | 0.85 | + | 0.29 |
| Portes et Barrières Total | 0.00 | 0.95 | + | 0.13 |
| Espaces Verts Total | 0.00 | 0.75 | + | 0.27 |
| Courrier et Colis total | 0.00 | 0.25 | – | 0.96 |
| Nettoyage Total | 0.00 | 0.19 | + | 0.04 |
| Déchets Total | 0.00 | 0.44 | + | 0.16 |
| Manutention Total | 0.00 | 0.21 | – | 0.64 |
On retrouve des résultats intéressants : la variable de vétusté 1 caractérisant les sites récents n’est pas significative de façon générale, mais la variable vétusté 3 représentant elle les sites anciens semble avoir un impact positif et significatif à un risque d’erreur de 5 % sur SLA Multi Techniques comme CVC et CFO ainsi que pour les SLA Multi Services Nettoyage et Management de Site. Sachant que la vétusté a un impact négatif sur les SLA les plus importants (CVC, Nettoyage, CFO …), nous pouvons donc conclure à un impact de la vétusté sur le prix du FM global.
Le nombre d’équipements :
Des listes d’équipements par site et par SLA ont été construites et tenues à jour par les managers de sites Thales. L’hétérogénéité des sources et l’inexistence de standards pour la construction de ces listes impliquent qu’une partie des données est incomplète ou inutilisable. Différentes listes d’équipements ne recensent pas les mêmes équipements pour un même SLA. Par exemple, pour le SLA Sécurité Incendie, une liste recensera toutes les têtes de sprinkler (qui se comptent la plupart du temps en centaines) quand d’autres ne les mentionnent pas. De plus, des listes ne font pas correspondre des SLA à des équipements, rendant leur catégorisation difficile si la nature de l’équipement n’est pas évidente. Toutes ces difficultés résultent d’une base de données de qualité médiocre.
Le nombre d’équipements a été déterminé comme plus pertinent que la puissance installée totale sur un site, sur les conseils de managers de site qui ont remarqué que le nombre était plus coûteux que la taille, car il impliquait plus d’interventions. On cherche également à mettre en évidence le coût de la massification des équipements : le coût d’un équipement supplémentaire est supérieur au coût moyen d’un équipement. Cela signifie qu’en plus de générer les coûts classiques (maintenances, énergie…), un équipement supplémentaire va générer des coûts additionnels dus à la massification (inefficiences, complexité des installations à équipements multiples…). Ces coûts additionnels vont augmenter avec le nombre d’équipements supplémentaires. Pour cela, introduire le carré de la variable d’équipement semble être la méthode adéquate. Nous n’observons pas de résultats notables : pour chaque régression, les 2 variables (nombre d’équipements et son carré) ne sont pas significatifs. Nous procédons donc à la méthode classique. Comme pour l’accord ou la vétusté, nous allons d’abord déterminer si le nombre d’équipements a un impact sur les différents prix des SLA correspondants, en contrôlant là aussi par la surface totale du site.
P-values | CVC | CFO | Entretien Bâtiment | Sécurité Incendie |
Nombre d’équipements | 0.54 | 0.95 | 0.12 | 0.04 |
Surface Totale | 0.00 | 0.00 | 0.00 | 0.00 |
| ||||
On rappelle que l’introduction de la variable de surface totale agit comme contrôle. Ainsi, même si les nombres d’équipements sont effectivement corrélés aux prix des SLA, leur non-significativité quand on introduit la surface montre que ces variables n’apportent pas d’information supplémentaire : le nombre d’équipement (pour chaque SLA) est corrélé avec la surface qui elle-même est corrélée avec le prix des SLA. Si l’on n’introduisait pas la surface dans le modèle, les coefficients associés à chaque nombre d’équipements seraient significatifs mais comprendraient un biais de spécification.
Localisation des sites à Paris / Province :
On étudie l’impact de la localisation des sites à l’Ile-de-France ou à la province. On s’attend à ce que la plupart des SLA soient plus chers pour des sites appartenant à Paris. On détermine une variable nommée Paris qui prendra comme valeur 1 lorsque le site appartient la région Ile-de-France, 0 sinon. Comme précédemment, on étudie premièrement les p-values :
| p-values | Surface Totale | Paris | Signe Paris |
|---|---|---|---|
| Management de Site Total | 0.00 | 0.00 | + |
| GTB Total | 0.00 | 0.54 | – |
| CVC Total | 0.00 | 0.40 | – |
| CFO Total | 0.00 | 0.74 | + |
| Sécurité Incendie Total | 0.00 | 0.14 | + |
| Installations de Sûreté Total | 0.00 | 0.30 | – |
| Contrôles Réglementaires Total | 0.00 | 0.55 | + |
| Entretien du Bâtiment Total | 0.00 | 0.76 | + |
| Appareils Elévateurs | 0.00 | 0.11 | + |
| Portes et Barrières Total | 0.00 | 0.31 | – |
| Espaces Verts Total | 0.00 | 0.46 | + |
| Courrier et Colis total | 0.00 | 0.00 | + |
| Nettoyage Total | 0.00 | 0.01 | + |
| Déchets Total | 0.00 | 0.26 | – |
| Manutention Total | 0.00 | 0.04 | + |
On note une colinéarité forte dans tous les modèles, ce qui n’empêche pas la variable Paris de montrer des résultats intéressants : selon les p-values, l’impact de la localisation à l’Ile-de-France est significatif et positif pour le prix des SLA Management de Site, Courrier et Colis, Nettoyage et Manutention, soient des SLA Multi-services. Cela signifie que pour 2 sites de même taille, l’un étant en Ile-de-France et l’autre en province, les prix de ces SLA pour le site d’Ile-de-France seront plus élevés que ceux du site de province. On peut supposer que le niveau des salaires, souvent plus élevés en Ile-de-France qu’en province, soit à l’origine de ces différences.
7. Conclusion
Malgré les difficultés rencontrées avec les données, les méthodes utilisées dans ce rapport montrent des résultats pertinents en termes de prédiction. Les SLA les plus importants (Nettoyage, CVC, Management) sont bien expliqués par nos modèles, et peuvent donc faire l’objet de prédictions assez précises compte tenu de la base de données. La régression linéaire étant une méthode assez aisément interprétable et reproductible, pourrait remplacer à terme les ratios actuellement utilisés dont nous avons précédemment pointé les défauts.
L’étude d’impact de variables supposées pertinentes comme l’accord ou la vétusté a permis d’établir un lien statistique entre prix du FM et vétusté : les sites anciens auront ainsi tendance à coûter plus cher que les sites récents. Nous avons également établi que, toutes choses égales par ailleurs, un site d’Ile-de-France aura des SLA Multi services (et donc un FM total) plus coûteux qu’un site de province. Enfin, nous n’avons pas trouvé de lien statistique entre l’accord des managers Thales et Prestataires et les prix des SLA, ainsi qu’entre le nombre d’équipements par site et par SLA et les prix des SLA correspondants.
Il semble important de préciser que l’importance de la surface dans nos résultats peut être biaisée par le fait que la surface est utilisée depuis des années pour contrôler la performance des sites, par le biais du ratio. Ainsi, les prix ont été lissés au fil des années dans le but d’être conformes aux surfaces. Il est fort probable que l’importance de la surface dans nos régressions soit augmentée artificiellement par cet effet, c’est-à-dire que si une autre méthode que les ratios par la surface avait été utilisée pour contrôler les prix des prestations, la surface ne jouerait pas un rôle aussi important dans nos régressions.
